Affine Finite Crystals

In this document we briefly explain the construction and implementation of the Kirillov–Reshetikhin crystals of [FourierEtAl2009].

Kirillov–Reshetikhin (KR) crystals are finite-dimensional affine crystals corresponding to Kirillov–Reshektikhin modules. They were first conjectured to exist in [HatayamaEtAl2001]. The proof of their existence for nonexceptional types was given in [OkadoSchilling2008] and their combinatorial models were constructed in [FourierEtAl2009]. Kirillov-Reshetikhin crystals \(B^{r,s}\) are indexed first by their type (like \(A_n^{(1)}\), \(B_n^{(1)}\), …) with underlying index set \(I = \{0,1,\ldots, n\}\) and two integers \(r\) and \(s\). The integers \(s\) only needs to satisfy \(s >0\), whereas \(r\) is a node of the finite Dynkin diagram \(r \in I \setminus \{0\}\).

Their construction relies on several cases which we discuss separately. In all cases when removing the zero arrows, the crystal decomposes as a (direct sum of) classical crystals which gives the crystal structure for the index set \(I_0 = \{ 1,2,\ldots, n\}\). Then the zero arrows are added by either exploiting a symmetry of the Dynkin diagram or by using embeddings of crystals.

Type \(A_n^{(1)}\)

The Dynkin diagram for affine type \(A\) has a rotational symmetry mapping \(\sigma: i \mapsto i+1\) where we view the indices modulo \(n+1\):

sage: C = CartanType(['A',3,1])
sage: C.dynkin_diagram()
0
O-------+
|       |
|       |
O---O---O
1   2   3
A3~

The classical decomposition of \(B^{r,s}\) is the \(A_n\) highest weight crystal \(B(s\omega_r)\) or equivalently the crystal of tableaux labelled by the rectangular partition \((s^r)\):

\[B^{r,s} \cong B(s\omega_r) \quad \text{as a } \{1,2,\ldots,n\}\text{-crystal}\]

In Sage we can see this via:

sage: K = crystals.KirillovReshetikhin(['A',3,1],1,1)
sage: K.classical_decomposition()
The crystal of tableaux of type ['A', 3] and shape(s) [[1]]
sage: K.list()
[[[1]], [[2]], [[3]], [[4]]]

sage: K = crystals.KirillovReshetikhin(['A',3,1],2,1)
sage: K.classical_decomposition()
The crystal of tableaux of type ['A', 3] and shape(s) [[1, 1]]

One can change between the classical and affine crystal using the methods lift and retract:

sage: K = crystals.KirillovReshetikhin(['A',3,1],2,1)
sage: b = K(rows=[[1],[3]]); type(b)
<class 'sage.combinat.crystals.kirillov_reshetikhin.KR_type_A_with_category.element_class'>
sage: b.lift()
[[1], [3]]
sage: type(b.lift())
<class 'sage.combinat.crystals.tensor_product.CrystalOfTableaux_with_category.element_class'>

sage: b = crystals.Tableaux(['A',3], shape = [1,1])(rows=[[1],[3]])
sage: K.retract(b)
[[1], [3]]
sage: type(K.retract(b))
<class 'sage.combinat.crystals.kirillov_reshetikhin.KR_type_A_with_category.element_class'>

The \(0\)-arrows are obtained using the analogue of \(\sigma\), called the promotion operator \(\mathrm{pr}\), on the level of crystals via:

\[ \begin{align}\begin{aligned}f_0 = \mathrm{pr}^{-1} \circ f_1 \circ \mathrm{pr}\\e_0 = \mathrm{pr}^{-1} \circ e_1 \circ \mathrm{pr}\end{aligned}\end{align} \]

In Sage this can be achieved as follows:

sage: K = crystals.KirillovReshetikhin(['A',3,1],2,1)
sage: b = K.module_generator(); b
[[1], [2]]
sage: b.f(0)
sage: b.e(0)
[[2], [4]]

sage: K.promotion()(b.lift())
[[2], [3]]
sage: K.promotion()(b.lift()).e(1)
[[1], [3]]
sage: K.promotion_inverse()(K.promotion()(b.lift()).e(1))
[[2], [4]]

KR crystals are level \(0\) crystals, meaning that the weight of all elements in these crystals is zero:

sage: K = crystals.KirillovReshetikhin(['A',3,1],2,1)
sage: b = K.module_generator(); b.weight()
-Lambda[0] + Lambda[2]
sage: b.weight().level()
0

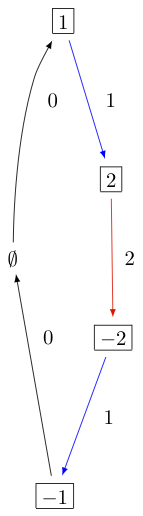
The KR crystal \(B^{1,1}\) of type \(A_2^{(1)}\) looks as follows:

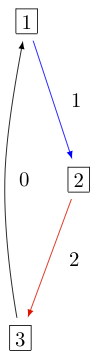
In Sage this can be obtained via:

sage: K = crystals.KirillovReshetikhin(['A',2,1],1,1)
sage: G = K.digraph()
sage: view(G, tightpage=True) # optional - dot2tex graphviz, not tested (opens external window)

Types \(D_n^{(1)}\), \(B_n^{(1)}\), \(A_{2n-1}^{(2)}\)

The Dynkin diagrams for types \(D_n^{(1)}\), \(B_n^{(1)}\), \(A_{2n-1}^{(2)}\) are invariant under interchanging nodes \(0\) and \(1\):

sage: n = 5
sage: C = CartanType(['D',n,1]); C.dynkin_diagram()
  0 O   O 5
    |   |
    |   |
O---O---O---O
1   2   3   4
D5~
sage: C = CartanType(['B',n,1]); C.dynkin_diagram()
    O 0
    |
    |
O---O---O---O=>=O
1   2   3   4   5
B5~
sage: C = CartanType(['A',2*n-1,2]); C.dynkin_diagram()
    O 0
    |
    |
O---O---O---O=<=O
1   2   3   4   5
B5~*

The underlying classical algebras obtained when removing node \(0\) are type \(\mathfrak{g}_0 = D_n, B_n, C_n\), respectively. The classical decomposition into a \(\mathfrak{g}_0\) crystal is a direct sum:

\[B^{r,s} \cong \bigoplus_\lambda B(\lambda) \quad \text{as a } \{1,2,\ldots,n\}\text{-crystal}\]

where \(\lambda\) is obtained from \(s\omega_r\) (or equivalently a rectangular partition of shape \((s^r)\)) by removing vertical dominoes. This in fact only holds in the ranges \(1\le r\le n-2\) for type \(D_n^{(1)}\), and \(1 \le r \le n\) for types \(B_n^{(1)}\) and \(A_{2n-1}^{(2)}\):

sage: K = crystals.KirillovReshetikhin(['D',6,1],4,2)
sage: K.classical_decomposition()
The crystal of tableaux of type ['D', 6] and shape(s)
 [[], [1, 1], [1, 1, 1, 1], [2, 2], [2, 2, 1, 1], [2, 2, 2, 2]]

For type \(B_n^{(1)}\) and \(r=n\), one needs to be aware that \(\omega_n\) is a spin weight and hence corresponds in the partition language to a column of height \(n\) and width \(1/2\):

sage: K = crystals.KirillovReshetikhin(['B',3,1],3,1)
sage: K.classical_decomposition()
The crystal of tableaux of type ['B', 3] and shape(s) [[1/2, 1/2, 1/2]]

As for type \(A_n^{(1)}\), the Dynkin automorphism induces a promotion-type operator \(\sigma\) on the level of crystals. In this case in can however happen that the automorphism changes between classical components:

sage: K = crystals.KirillovReshetikhin(['D',4,1],2,1)
sage: b = K.module_generator(); b
[[1], [2]]
sage: K.automorphism(b)
[[2], [-1]]
sage: b = K(rows=[[2],[-2]])
sage: K.automorphism(b)
[]

This operator \(\sigma\) is used to define the affine crystal operators:

\[ \begin{align}\begin{aligned}f_0 = \sigma \circ f_1 \circ \sigma\\e_0 = \sigma \circ e_1 \circ \sigma\end{aligned}\end{align} \]

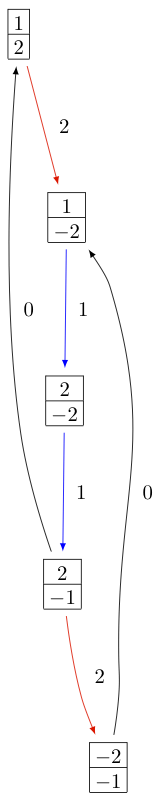
The KR crystals \(B^{1,1}\) of types \(D_3^{(1)}\), \(B_2^{(1)}\), and \(A_5^{(2)}\) are, respectively:

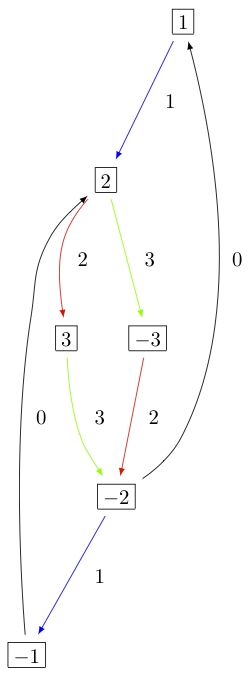
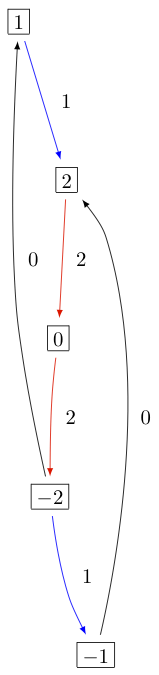
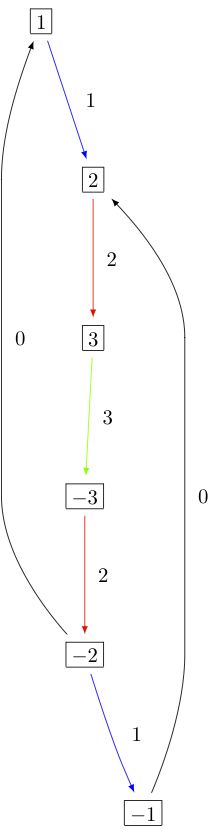
Type \(C_n^{(1)}\)

The Dynkin diagram of type \(C_n^{(1)}\) has a symmetry \(\sigma(i) = n-i\):

sage: C = CartanType(['C',4,1]); C.dynkin_diagram()
O=>=O---O---O=<=O
0   1   2   3   4
C4~

The classical subalgebra when removing the 0 node is of type \(C_n\).

However, in this case the crystal \(B^{r,s}\) is not constructed using \(\sigma\), but rather using a virtual crystal construction. \(B^{r,s}\) of type \(C_n^{(1)}\) is realized inside \(\hat{V}^{r,s}\) of type \(A_{2n+1}^{(2)}\) using:

\[ \begin{align}\begin{aligned}e_0 = \hat{e}_0 \hat{e}_1 \quad \text{and} \quad e_i = \hat{e}_{i+1} \quad \text{for} \quad 1\le i\le n\\f_0 = \hat{f}_0 \hat{f}_1 \quad \text{and} \quad f_i = \hat{f}_{i+1} \quad \text{for} \quad 1\le i\le n\end{aligned}\end{align} \]

where \(\hat{e}_i\) and \(\hat{f}_i\) are the crystal operator in the ambient crystal \(\hat{V}^{r,s}\):

sage: K = crystals.KirillovReshetikhin(['C',3,1],1,2); K.ambient_crystal()
Kirillov-Reshetikhin crystal of type ['B', 4, 1]^* with (r,s)=(1,2)

The classical decomposition for \(1 \le r < n\) is given by:

\[B^{r,s} \cong \bigoplus_\lambda B(\lambda) \quad \text{as a } \{1,2,\ldots,n\}\text{-crystal}\]

where \(\lambda\) is obtained from \(s\omega_r\) (or equivalently a rectangular partition of shape \((s^r)\)) by removing horizontal dominoes:

sage: K = crystals.KirillovReshetikhin(['C',3,1],2,4)
sage: K.classical_decomposition()
The crystal of tableaux of type ['C', 3] and shape(s) [[], [2], [4], [2, 2], [4, 2], [4, 4]]

The KR crystal \(B^{1,1}\) of type \(C_2^{(1)}\) looks as follows:

Types \(D_{n+1}^{(2)}\), \(A_{2n}^{(2)}\)

The Dynkin diagrams of types \(D_{n+1}^{(2)}\) and \(A_{2n}^{(2)}\) look as follows:

sage: C = CartanType(['D',5,2]); C.dynkin_diagram()
O=<=O---O---O=>=O
0   1   2   3   4
C4~*

sage: C = CartanType(['A',8,2]); C.dynkin_diagram()
O=<=O---O---O=<=O
0   1   2   3   4
BC4~

The classical subdiagram is of type \(B_n\) for type \(D_{n+1}^{(2)}\) and of type \(C_n\) for type \(A_{2n}^{(2)}\). The classical decomposition for these KR crystals for \(1\le r < n\) for type \(D_{n+1}^{(2)}\) and \(1 \le r \le n\) for type \(A_{2n}^{(2)}\) is given by:

\[B^{r,s} \cong \bigoplus_\lambda B(\lambda) \quad \text{as a } \{1,2,\ldots,n\}\text{-crystal}\]

where \(\lambda\) is obtained from \(s\omega_r\) (or equivalently a rectangular partition of shape \((s^r)\)) by removing single boxes:

sage: K = crystals.KirillovReshetikhin(['D',5,2],2,2)
sage: K.classical_decomposition()
The crystal of tableaux of type ['B', 4] and shape(s) [[], [1], [2], [1, 1], [2, 1], [2, 2]]

sage: K = crystals.KirillovReshetikhin(['A',8,2],2,2)
sage: K.classical_decomposition()
The crystal of tableaux of type ['C', 4] and shape(s) [[], [1], [2], [1, 1], [2, 1], [2, 2]]

The KR crystals are constructed using an injective map into a KR crystal of type \(C_n^{(1)}\)

\[S : B^{r,s} \to B^{r,2s}_{C_n^{(1)}} \quad \text{such that } S(e_ib) = e_i^{m_i}S(b) \text{ and } S(f_ib) = f_i^{m_i}S(b)\]

where

\[(m_0,\ldots,m_n) = (1,2,\ldots,2,1) \text{ for type } D_{n+1}^{(2)} \quad \text{and} \quad (1,2,\ldots,2,2) \text{ for type } A_{2n}^{(2)}.\]

sage: K = crystals.KirillovReshetikhin(['D',5,2],1,2); K.ambient_crystal()
Kirillov-Reshetikhin crystal of type ['C', 4, 1] with (r,s)=(1,4)
sage: K = crystals.KirillovReshetikhin(['A',8,2],1,2); K.ambient_crystal()
Kirillov-Reshetikhin crystal of type ['C', 4, 1] with (r,s)=(1,4)

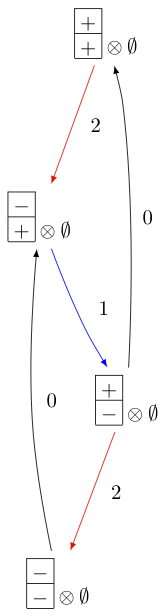
The KR crystals \(B^{1,1}\) of type \(D_3^{(2)}\) and \(A_4^{(2)}\) look as follows:

As you can see from the Dynkin diagram for type \(A_{2n}^{(2)}\), mapping the nodes \(i\mapsto n-i\) yields the same diagram, but with relabelled nodes. In this case the classical subdiagram is of type \(B_n\) instead of \(C_n\). One can also construct the KR crystal \(B^{r,s}\) of type \(A_{2n}^{(2)}\) based on this classical decomposition. In this case the classical decomposition is the sum over all weights obtained from \(s \omega_r\) by removing horizontal dominoes:

sage: C = CartanType(['A',6,2]).dual()
sage: Kdual = crystals.KirillovReshetikhin(C,2,2)
sage: Kdual.classical_decomposition()
The crystal of tableaux of type ['B', 3] and shape(s) [[], [2], [2, 2]]

Looking at the picture, one can see that this implementation is isomorphic to the other implementation based on the \(C_n\) decomposition up to a relabeling of the arrows:

sage: C = CartanType(['A',4,2])
sage: K = crystals.KirillovReshetikhin(C,1,1)
sage: Kdual = crystals.KirillovReshetikhin(C.dual(),1,1)
sage: G = K.digraph()
sage: Gdual = Kdual.digraph()
sage: f = { 1:1, 0:2, 2:0 }
sage: for u,v,label in Gdual.edges():
....:     Gdual.set_edge_label(u,v,f[label])
sage: G.is_isomorphic(Gdual, edge_labels = True)
True

Exceptional nodes

The KR crystals \(B^{n,s}\) for types \(C_n^{(1)}\) and \(D_{n+1}^{(2)}\) were excluded from the above discussion. They are associated to the exceptional node \(r=n\) and in this case the classical decomposition is irreducible:

\[B^{n,s} \cong B(s\omega_n).\]

In Sage:

sage: K = crystals.KirillovReshetikhin(['C',2,1],2,1)
sage: K.classical_decomposition()
The crystal of tableaux of type ['C', 2] and shape(s) [[1, 1]]

sage: K = crystals.KirillovReshetikhin(['D',3,2],2,1)
sage: K.classical_decomposition()
The crystal of tableaux of type ['B', 2] and shape(s) [[1/2, 1/2]]

The KR crystals \(B^{n,s}\) and \(B^{n-1,s}\) of type \(D_n^{(1)}\) are also special. They decompose as:

\[B^{n,s} \cong B(s\omega_n) \quad \text{ and } \quad B^{n-1,s} \cong B(s\omega_{n-1}).\]

sage: K = crystals.KirillovReshetikhin(['D',4,1],4,1)
sage: K.classical_decomposition()
The crystal of tableaux of type ['D', 4] and shape(s) [[1/2, 1/2, 1/2, 1/2]]
sage: K = crystals.KirillovReshetikhin(['D',4,1],3,1)
sage: K.classical_decomposition()
The crystal of tableaux of type ['D', 4] and shape(s) [[1/2, 1/2, 1/2, -1/2]]

Type \(E_6^{(1)}\)

In [JonesEtAl2010] the KR crystals \(B^{r,s}\) for \(r=1,2,6\) in type \(E_6^{(1)}\) were constructed exploiting again a Dynkin diagram automorphism, namely the automorphism \(\sigma\) of order 3 which maps \(0\mapsto 1 \mapsto 6 \mapsto 0\):

sage: C = CartanType(['E',6,1]); C.dynkin_diagram()
        O 0
        |
        |
        O 2
        |
        |
O---O---O---O---O
1   3   4   5   6
E6~

The crystals \(B^{1,s}\) and \(B^{6,s}\) are irreducible as classical crystals:

sage: K = crystals.KirillovReshetikhin(['E',6,1],1,1)
sage: K.classical_decomposition()
Direct sum of the crystals Family (Finite dimensional highest weight crystal of type ['E', 6] and highest weight Lambda[1],)
sage: K = crystals.KirillovReshetikhin(['E',6,1],6,1)
sage: K.classical_decomposition()
Direct sum of the crystals Family (Finite dimensional highest weight crystal of type ['E', 6] and highest weight Lambda[6],)

whereas for the adjoint node \(r=2\) we have the decomposition

\[B^{2,s} \cong \bigoplus_{k=0}^s B(k\omega_2)\]

sage: K = crystals.KirillovReshetikhin(['E',6,1],2,1)
sage: K.classical_decomposition()
Direct sum of the crystals Family (Finite dimensional highest weight crystal of type ['E', 6] and highest weight 0,
Finite dimensional highest weight crystal of type ['E', 6] and highest weight Lambda[2])

The promotion operator on the crystal corresponding to \(\sigma\) can be calculated explicitly:

sage: K = crystals.KirillovReshetikhin(['E',6,1],1,1)
sage: promotion = K.promotion()
sage: u = K.module_generator(); u
[(1,)]
sage: promotion(u.lift())
[(-1, 6)]

The crystal \(B^{1,1}\) is already of dimension 27. The elements \(b\) of this crystal are labelled by tuples which specify their nonzero \(\phi_i(b)\) and \(\epsilon_i(b)\). For example, \([-6,2]\) indicates that \(\phi_2([-6,2]) = \epsilon_6([-6,2]) = 1\) and all others are equal to zero:

sage: K = crystals.KirillovReshetikhin(['E',6,1],1,1)
sage: K.cardinality()
27

Single column KR crystals

A single column KR crystal is \(B^{r,1}\) for any \(r \in I_0\).

In [LNSSS14I] and [LNSSS14II], it was shown that single column KR crystals can be constructed by projecting level 0 crystals of LS paths onto the classical weight lattice. We first verify that we do get an isomorphic crystal for \(B^{1,1}\) in type \(E_6^{(1)}\):

sage: K = crystals.KirillovReshetikhin(['E',6,1], 1,1)
sage: K2 = crystals.kirillov_reshetikhin.LSPaths(['E',6,1], 1,1)
sage: K.digraph().is_isomorphic(K2.digraph(), edge_labels=True)
True

Here is an example in \(E_8^{(1)}\) and we calculate its classical decomposition:

sage: K = crystals.kirillov_reshetikhin.LSPaths(['E',8,1], 8,1)
sage: K.cardinality()
249
sage: L = [x for x in K if x.is_highest_weight([1,2,3,4,5,6,7,8])]
sage: [x.weight() for x in L]
[-2*Lambda[0] + Lambda[8], 0]

Applications

An important notion for finite-dimensional affine crystals is perfectness. The crucial property is that a crystal \(B\) is perfect of level \(\ell\) if there is a bijection between level \(\ell\) dominant weights and elements in

\[B_{\mathrm{min}} = \{ b \in B \mid \mathrm{lev}(\varphi(b)) = \ell \}\;.\]

For a precise definition of perfect crystals see [HongKang2002] . In [FourierEtAl2010] it was proven that for the nonexceptional types \(B^{r,s}\) is perfect as long as \(s/c_r\) is an integer. Here \(c_r=1\) except \(c_r=2\) for \(1 \le r < n\) in type \(C_n^{(1)}\) and \(r=n\) in type \(B_n^{(1)}\).

Here we verify this using Sage for \(B^{1,1}\) of type \(C_3^{(1)}\):

sage: K = crystals.KirillovReshetikhin(['C',3,1],1,1)
sage: Lambda = K.weight_lattice_realization().fundamental_weights(); Lambda
Finite family {0: Lambda[0], 1: Lambda[1], 2: Lambda[2], 3: Lambda[3]}
sage: [w.level() for w in Lambda]
[1, 1, 1, 1]
sage: Bmin = [b for b in K if b.Phi().level() == 1 ]; Bmin
[[[1]], [[2]], [[3]], [[-3]], [[-2]], [[-1]]]
sage: [b.Phi() for b in Bmin]
[Lambda[1], Lambda[2], Lambda[3], Lambda[2], Lambda[1], Lambda[0]]

As you can see, both \(b=1\) and \(b=-2\) satisfy \(\varphi(b)=\Lambda_1\). Hence there is no bijection between the minimal elements in \(B_{\mathrm{min}}\) and level 1 weights. Therefore, \(B^{1,1}\) of type \(C_3^{(1)}\) is not perfect. However, \(B^{1,2}\) of type \(C_n^{(1)}\) is a perfect crystal:

sage: K = crystals.KirillovReshetikhin(['C',3,1],1,2)
sage: Lambda = K.weight_lattice_realization().fundamental_weights()
sage: Bmin = [b for b in K if b.Phi().level() == 1 ]
sage: [b.Phi() for b in Bmin]
[Lambda[0], Lambda[3], Lambda[2], Lambda[1]]

Perfect crystals can be used to construct infinite-dimensional highest weight crystals and Demazure crystals using the Kyoto path model [KKMMNN1992]. We construct Example 10.6.5 in [HongKang2002]:

sage: K = crystals.KirillovReshetikhin(['A',1,1], 1,1)
sage: La = RootSystem(['A',1,1]).weight_lattice().fundamental_weights()
sage: B = crystals.KyotoPathModel(K, La[0])
sage: B.highest_weight_vector()
[[[2]]]

sage: K = crystals.KirillovReshetikhin(['A',2,1], 1,1)
sage: La = RootSystem(['A',2,1]).weight_lattice().fundamental_weights()
sage: B = crystals.KyotoPathModel(K, La[0])
sage: B.highest_weight_vector()
[[[3]]]

sage: K = crystals.KirillovReshetikhin(['C',2,1], 2,1)
sage: La = RootSystem(['C',2,1]).weight_lattice().fundamental_weights()
sage: B = crystals.KyotoPathModel(K, La[1])
sage: B.highest_weight_vector()
[[[2], [-2]]]

Energy function and one-dimensional configuration sum

For tensor products of Kirillov-Reshehtikhin crystals, there also exists the important notion of the energy function. It can be defined as the sum of certain local energy functions and the \(R\)-matrix. In Theorem 7.5 in [SchillingTingley2011] it was shown that for perfect crystals of the same level the energy \(D(b)\) is the same as the affine grading (up to a normalization). The affine grading is defined as the minimal number of applications of \(e_0\) to \(b\) to reach a ground state path. Computationally, this algorithm is a lot more efficient than the computation involving the \(R\)-matrix and has been implemented in Sage:

sage: K = crystals.KirillovReshetikhin(['A',2,1],1,1)
sage: T = crystals.TensorProduct(K,K,K)
sage: hw = [b for b in T if all(b.epsilon(i)==0 for i in [1,2])]
sage: for b in hw:
....:     print("{} {}".format(b, b.energy_function()))
[[[1]], [[1]], [[1]]] 0
[[[1]], [[2]], [[1]]] 2
[[[2]], [[1]], [[1]]] 1
[[[3]], [[2]], [[1]]] 3

The affine grading can be computed even for nonperfect crystals:

sage: K = crystals.KirillovReshetikhin(['C',4,1],1,2)
sage: K1 = crystals.KirillovReshetikhin(['C',4,1],1,1)
sage: T = crystals.TensorProduct(K,K1)
sage: hw = [b for b in T if all(b.epsilon(i)==0 for i in [1,2,3,4])]
sage: for b in hw:
....:     print("{} {}".format(b, b.affine_grading()))
[[], [[1]]] 1
[[[1, 1]], [[1]]] 2
[[[1, 2]], [[1]]] 1
[[[1, -1]], [[1]]] 0

The one-dimensional configuration sum of a crystal \(B\) is the graded sum by energy of the weight of all elements \(b \in B\):

\[X(B) = \sum_{b \in B} x^{\mathrm{weight}(b)} q^{D(b)}\]

Here is an example of how you can compute the one-dimensional configuration sum in Sage:

sage: K = crystals.KirillovReshetikhin(['A',2,1],1,1)
sage: T = crystals.TensorProduct(K,K)
sage: T.one_dimensional_configuration_sum()
B[-2*Lambda[1] + 2*Lambda[2]] + (q+1)*B[-Lambda[1]]
 + (q+1)*B[Lambda[1] - Lambda[2]] + B[2*Lambda[1]]
 + B[-2*Lambda[2]] + (q+1)*B[Lambda[2]]