Un Tour Por Sage

Este es un tour por Sage que sigue de cerca al Tour Por Mathematica que está al comienzo del Libro de Mathematica.

Sage Como Una Calculadora

La línea de comandos de Sage tiene un prompt sage:; no necesitas agregarlo. Si utilizas el Notebook de Sage, entonces coloca todo lo que haya después del prompt sage: en una celda de entrada de datos, y presiona shift-enter para calcular la salida correspondiente.

sage: 3 + 5
8

El acento circunflejo ^ significa «elevar a la potencia».

sage: 57.1 ^ 100
4.60904368661396e175

Calculamos el inverso de una matriz de \(2 \times 2\) en Sage.

sage: matrix([[1,2], [3,4]])^(-1)
[  -2    1]
[ 3/2 -1/2]

Aquí integramos una función simple.

sage: x = var('x')   # crea una variable simbólica
sage: integrate(sqrt(x)*sqrt(1+x), x)
1/4*((x + 1)^(3/2)/x^(3/2) + sqrt(x + 1)/sqrt(x))/((x + 1)^2/x^2 - 2*(x + 1)/x + 1) - 1/8*log(sqrt(x + 1)/sqrt(x) + 1) + 1/8*log(sqrt(x + 1)/sqrt(x) - 1)

Esto le pide a Sage que resuelva una ecuación cuadrática. El símbolo == representa igualdad en Sage.

sage: a = var('a')
sage: S = solve(x^2 + x == a, x); S
[x == -1/2*sqrt(4*a + 1) - 1/2, x == 1/2*sqrt(4*a + 1) - 1/2]

El resultado es una lista de igualdades.

sage: S[0].rhs()
-1/2*sqrt(4*a + 1) - 1/2
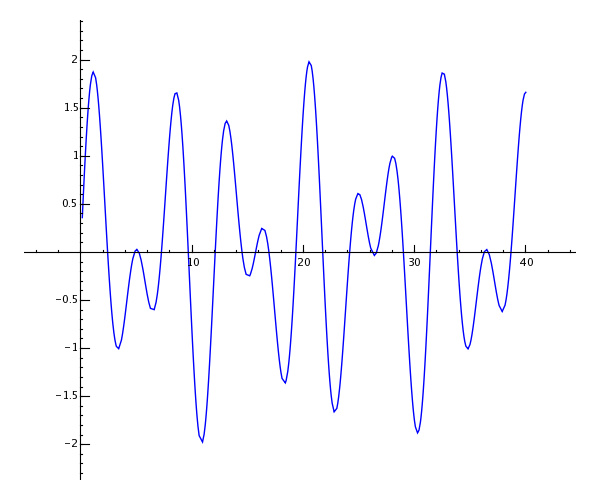
sage: show(plot(sin(x) + sin(1.6*x), 0, 40))

Potencia de Cálculo Con Sage

Primero creamos una matriz de \(500 \times 500\) con números aleatorios.

sage: m = random_matrix(RDF,500)

Sage tarda unos cuantos segundos en calcular los valores propios de la matriz y mostrarlos.

sage: e = m.eigenvalues()  #alrededor de 2 segundos
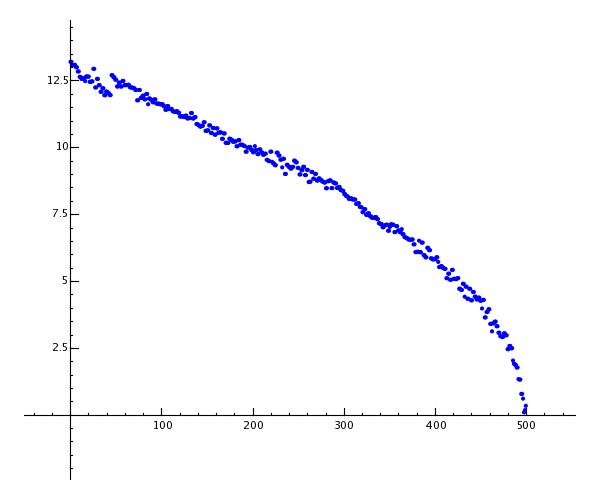
sage: w = [(i, abs(e[i])) for i in range(len(e))]
sage: show(points(w))

Gracias a la Biblioteca GNU de Multiprecisión (GMP), Sage puede manejar números muy grandes, hasta números con millones o billones de dígitos.

sage: factorial(100)
93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000
sage: n = factorial(1000000)  # alrededor de 2.5 segundos

Esto calcula al menos 100 digitos de \(\pi\).

sage: N(pi, digits=100)
3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117068

Esto le pide a Sage que factorice un polinomio en dos variables.

sage: R.<x,y> = QQ[]
sage: F = factor(x^99 + y^99)
sage: F
(x + y) * (x^2 - x*y + y^2) * (x^6 - x^3*y^3 + y^6) *
(x^10 - x^9*y + x^8*y^2 - x^7*y^3 + x^6*y^4 - x^5*y^5 +
 x^4*y^6 - x^3*y^7 + x^2*y^8 - x*y^9 + y^10) *
(x^20 + x^19*y - x^17*y^3 - x^16*y^4 + x^14*y^6 + x^13*y^7 -
 x^11*y^9 - x^10*y^10 - x^9*y^11 + x^7*y^13 + x^6*y^14 -
 x^4*y^16 - x^3*y^17 + x*y^19 + y^20) * (x^60 + x^57*y^3 -
 x^51*y^9 - x^48*y^12 + x^42*y^18 + x^39*y^21 - x^33*y^27 -
 x^30*y^30 - x^27*y^33 + x^21*y^39 + x^18*y^42 - x^12*y^48 -
 x^9*y^51 + x^3*y^57 + y^60)
sage: F.expand()
x^99 + y^99

Sage tarda menos de 5 segundos en calcular el número de maneras de repartir cien millones como una suma de enteros positivos.

sage: z = Partitions(10^8).cardinality() # alrededor de 4.5 segundos
sage: str(z)[:40]
'1760517045946249141360373894679135204009'

Accediendo a Distintos Algoritmos en Sage

Cada vez que usas Sage, estás accediendo a una de las más grandes colecciones de algoritmos computacionales de código abierto del mundo entero.