Elementary crystals

Note

Each of these crystals will work with any Cartan matrix input (with weights from the weight lattice corresponding to the Cartan matrix given).

T-crystal

Let \(\lambda\) be a weight. As defined in [Kashiwara1993] (see, also, [Kashiwara1995]) the crystal \(T_{\lambda} = \{ t_{\lambda} \}\) is a single element crystal with the crystal structure defined by

\[\mathrm{wt}(t_\lambda) = \lambda, \quad e_i t_{\lambda} = f_i t_{\lambda} = 0, \quad \varepsilon_i(t_{\lambda}) = \varphi_i(t_{\lambda}) = -\infty.\]

The crystal \(T_{\lambda}\) shifts the weights of the vertices in a crystal \(B\) by \(\lambda\) when tensored with \(B\), but leaves the graph structure of \(B\) unchanged. That is, for all \(b \in B\), we have \(\mathrm{wt}(t_\lambda \otimes b) = \mathrm{wt}(b) + \lambda\):

sage: B = crystals.Tableaux(['A',2],shape=[2,1])
sage: T = crystals.elementary.T(['A',2], B.Lambda()[1] + B.Lambda()[2])
sage: V = crystals.TensorProduct(T,B)
sage: for x in V:
....:     print(x.weight())
....:
(4, 2, 0)
(3, 3, 0)
(3, 2, 1)
(3, 1, 2)
(2, 2, 2)
(4, 1, 1)
(3, 2, 1)
(2, 3, 1)
sage: for x in B:
....:     print(x.weight() + T[0].weight())
....:
(4, 2, 0)
(3, 3, 0)
(3, 2, 1)
(3, 1, 2)
(2, 2, 2)
(4, 1, 1)
(3, 2, 1)
(2, 3, 1)

Warning

Sage uses the opposite convention for the tensor product rule to Kashiwara’s definition, so care must be taken when comparing the examples here with Kashiwara’s papers.

Here is an example using a hyperbolic Cartan matrix:

sage: A = CartanMatrix([[2,-4],[-4,2]])
sage: La = RootSystem(A).weight_lattice().fundamental_weights()
sage: La
Finite family {0: Lambda[0], 1: Lambda[1]}
sage: T = crystals.elementary.T(A,La[1])
sage: T
The T crystal of type [ 2 -4]
[-4  2] and weight Lambda[1]

C-crystal

Defined in [Kashiwara1993], the component crystal \(C = \{c\}\) is the single element crystal whose crystal structure is defined by

\[\mathrm{wt}(c) = 0, \quad e_i c = f_i c = 0, \quad \varepsilon_i(c) = \varphi_i(c) = 0.\]

Note \(C \cong B(0)\), where \(B(0)\) is the highest weight crystal of highest weight \(0\).

The crystal \(C \otimes T_\mu\) is useful when finding subcrystals inside irreducible highest weight crystals \(B(\lambda)\) where \(\lambda\) is larger than \(\mu\) in the lexicographic order. For example:

sage: P = RootSystem("C2").weight_lattice()
sage: La = P.fundamental_weights()
sage: h = P.simple_coroots()
sage: T = crystals.elementary.T("C2", 2*La[1])
sage: C = crystals.elementary.Component(P)
sage: B = crystals.TensorProduct(C,T)
sage: b = B(C[0],T[0])
sage: for i in B.index_set(): print(b.epsilon(i))
-2
0
sage: for i in B.index_set(): print(b.phi(i))
0
0
sage: for i in B.index_set(): print(b.f(i))
None
None
sage: for i in B.index_set(): print(b.e(i))
None
None

This new crystal can be summarized into the R-crystal below.

R-crystal

For a fixed weight \(\lambda\), the crystal \(R_{\lambda} = \{ r_{\lambda} \}\) is a single element crystal with the crystal structure defined by

\[\mathrm{wt}(r_{\lambda}) = \lambda, \quad e_i r_{\lambda} = f_i r_{\lambda} = 0, \quad \varepsilon_i(r_{\lambda}) = -\langle h_i, \lambda\rangle, \quad \varphi_i(r_{\lambda}) = 0,\]

where \(\{h_i\}\) are the simple coroots. See page 146 [Joseph1995], for example, for more details. (Note that in [Joseph1995], this crystal is denoted by \(S_\lambda\).)

Tensoring \(R_{\lambda}\) with a crystal \(B\) results in shifting the weights of the vertices in \(B\) by \(\lambda\) and may also cut a subset out of the original graph of \(B\).

Warning

Sage uses the opposite convention for the tensor product rule to Kashiwara’s definition, so care must be taken when comparing the examples here with some of the literature.

For example, suppose \(\mu \le \lambda\) in lexicographic ordering on weights, and one wants to see \(B(\mu)\) as a subcrystal of \(B(\lambda)\). Then \(B(\mu)\) may be realized as the connected component of \(R_{\mu-\lambda}\otimes B(\lambda)\) containing the highest weight \(r_{\mu-\lambda} \otimes u_\lambda\), where \(u_\lambda\) is the highest weight vector in \(B(\lambda)\):

sage: La = RootSystem(['B',4]).weight_lattice().fundamental_weights()
sage: Bla = crystals.NakajimaMonomials(['B',4], La[1]+La[2])
sage: Bmu = crystals.NakajimaMonomials(['B',4], La[1])
sage: R = crystals.elementary.R(['B',4], -La[2])
sage: T = crystals.TensorProduct(R,Bla)
sage: mg = mg = T(R[0], Bla.module_generators[0])
sage: S = T.subcrystal(generators=[mg])
sage: G = T.digraph(subset=S)
sage: Bmu.digraph().is_isomorphic(G, edge_labels=True)
True
sage: view(G, tightpage=True) # optional - dot2tex graphviz, not tested (opens external window)

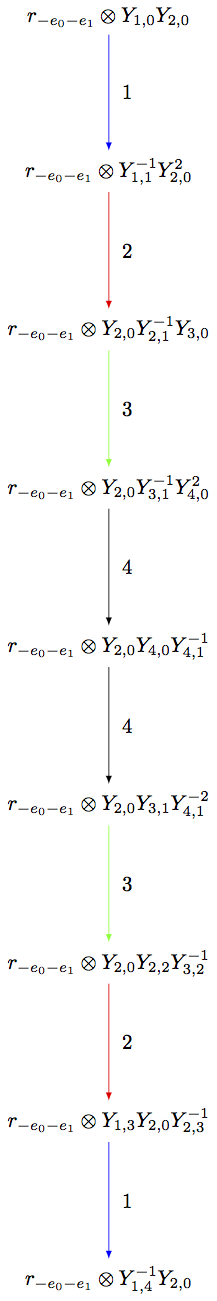
\(i\)-th elementary crystal

For \(i\) an element of the index set of type \(X\), the crystal \(B_i\) of type \(X\) is the set

\[B_i = \{ b_i(m) : m \in \ZZ \},\]

where the crystal structure is given by \(\mathrm{wt}\bigl(b_i(m)\bigr) = m\alpha_i\) and

\[\begin{split}\begin{aligned} \varphi_j\bigl(b_i(m)\bigr) &= \begin{cases} m & \text{ if } j=i, \\ -\infty & \text{ if } j\neq i, \end{cases} & \varepsilon_j\bigl(b_i(m)\bigr) &= \begin{cases} -m & \text{ if } j=i, \\ -\infty & \text{ if } j\neq i, \end{cases} \\ f_j b_i(m) &= \begin{cases} b_i(m-1) & \text{ if } j=i, \\ 0 & \text{ if } j\neq i, \end{cases} & e_j b_i(m) &= \begin{cases} b_i(m+1) & \text{ if } j=i, \\ 0 & \text{ if } j\neq i. \end{cases} \end{aligned}\end{split}\]

See [Kashiwara1993] or [Kashiwara1995] for more information. Here is an example:

sage: B = crystals.elementary.Elementary("A2",1)
sage: S = B.subcrystal(max_depth=4, generators=[B(0)])
sage: sorted(s for s in S)
[-4, -3, -2, -1, 0, 1, 2, 3, 4]
sage: G = B.digraph(subset=S)
sage: view(G, tightpage=True) # optional - dot2tex graphviz, not tested (opens external window)

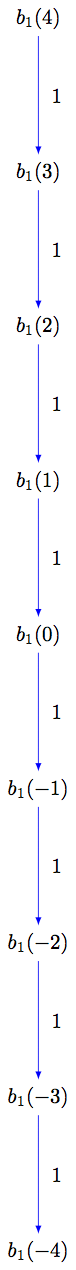
Warning

To reiterate, Sage uses the opposite convention for the tensor product rule to Kashiwara’s definition. In particular, using Sage’s convention, one has \(T_\lambda \otimes B_i \cong B_i \otimes T_{s_i\lambda}\), where \(s_i\) is the \(i\)-th simple reflection.